Monte Carlo integration is numerical integration using random numbers for the approximate evaluation of definite integrals.
For multidimensional definite integration:
 Suppose that the sample has size N and denote the points in the sample by
Suppose that the sample has size N and denote the points in the sample by  . Then the estimate for the integral is given by
. Then the estimate for the integral is given by  ,
,
 denotes the sample mean of the integrand and V is volume.
denotes the sample mean of the integrand and V is volume.The variance of the function can be estimated using
- Matlab code for Monte Carlo 3D integration:
%e.g. MC3D(inline('x.+2*y.*z'), [0 1 0 1 0 1], 5000)
function MC3D(fun, range, N)
B = range;
R = rand(3, N);
%Set the random samplings to the correct intervals
R(1, :) = (B(2)-B(1))*R(1, :)+ B(1);
R(2, :) = R(2, :)*(B(4) - B(3)) + B(3);
R(3, :) = R(3, :)*(B(6) - B(5)) + B(5);
Volume = (B(2)-B(1))*(B(4)-B(3))*(B(6)-B(5));
s = feval(fun, R(1,:), R(2,:), R(3,:));
total = sum(s);
avgF = total/N;
Int_result = avgF*Volume;
fprintf('Approximation: %f',Int_result );
C++ code for MC integration 4/(1.+x*x) from [0 1]
#include <cmath> #include <iostream> using namespace std; // Here we define various functions called by the main program // this function defines the function to integrate double func(double x); // Main function begins here int main() { int i, n; long idum; double crude_mc, sum_sigma, fx, variance, exact; printf("Read in the number of Monte-Carlo samples\n"); scanf("%d", &n); crude_mc = sum_sigma=0. ; idum=-1 ; exact=acos(-1.); // evaluate the integral with a crude Monte-Carlo method for ( i = 1; i <= n; i++){ double x=rand()/(RAND_MAX+1.0); fx=func(x); crude_mc += fx; sum_sigma += fx*fx; } crude_mc = crude_mc/((double) n ); sum_sigma = sum_sigma/((double) n ); variance=sum_sigma-crude_mc*crude_mc; // final output
printf("%d var= %12.5E Inum= %12.5E pi= %12.5E\n", n, variance, crude_mc, exact);
return 0;
} // end of main program
// this function defines the function to integratedouble func(double x)
{
double value;
value = 4/(1.+x*x);
return value;
} // end of function to evaluate 2. variational Monte Carlo (VMC) Variation Monte Carlo is a quantum Monte Carlo method that applies
the variational method to approximate the ground state of the system.The expectation value necessary can be written in the x representation as

QWalk is a program developed to perform quantum Monte Carlo calculations of electronic structure in molecules and solids. It has been written from the ground up in C++ incorporating a modular approach that makes it extremely extensible as a research vehicle. It has also been written specifically with large-scale parallel processing in mind, making it usable on (and portable to) the fastest computers in the world.
QWalk is freely available for download
| Tutorial | |||
| Manual | |||
| Download | |||
| History | |||
| Publications |
What's the deal with the version numbers?

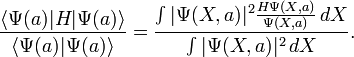
Ni Hau,
ReplyDeleteMuchas Gracias Mi Amigo! You make learning so effortless. Anyone can follow you and I would not mind following you to the moon coz I know you are like my north star.
I have a program like below
Python Code: (Double-click to select all)
1
2
3
4
5
6
7
8
9 import pytablewriter
writer = pytablewriter.MarkdownTableWriter()
writer.table_name = "example_table"
writer.header_list = ["SERVICE NAME", "TEAM NAME", "CI OWNER", "SECONDARY CONTACT", "PAYCHECK NAME", "DEV", "DEVII","QA", "STAGE", "PROD", "PROD"]
writer.value_matrix = [
["accommodation", "POSE", "Donker","Khavarian","Acc", "Yes", "Yes", "Yes","Yes","Yes","Yes"],
["activity-entity", "Reg","Chang", "John", "TER", "Yes", "Yes", "Yes", "Yes", "Yes", "Yes"],
]
writer.write_table()
This works well.. but my requirment is
1. I have hardcoded values for value_
matrix above..instead I have a csv file which has around 340 rows , instead of hardcoding these into program , i need to read that file and store all rows in the value_matrix
2. now once we have all 340 rows are written into matrix, I want to pass SERVICE NAME which is first field in csv i.e in above example code accommodation as run time paramater so that it will output only that row...
THANK YOU!! This saved my butt today, I’m immensely grateful.
Shukran,
Ajeeth